
Therefore we can conclude that triangle KLG is an isosceles triangles. We can use the angle measure tool to see that and have equal measure and that segments GK and GL have equal length. We then use the segment tool to construct lines KL, LG, and GK. The point of intersection between the perpendicular line and ray GH is labeled K and the point of intersection between the perpendicular line and ray GI is labeled L. To find the ratio number of the hypotenuse h, we.
Triangle isosceles iso#
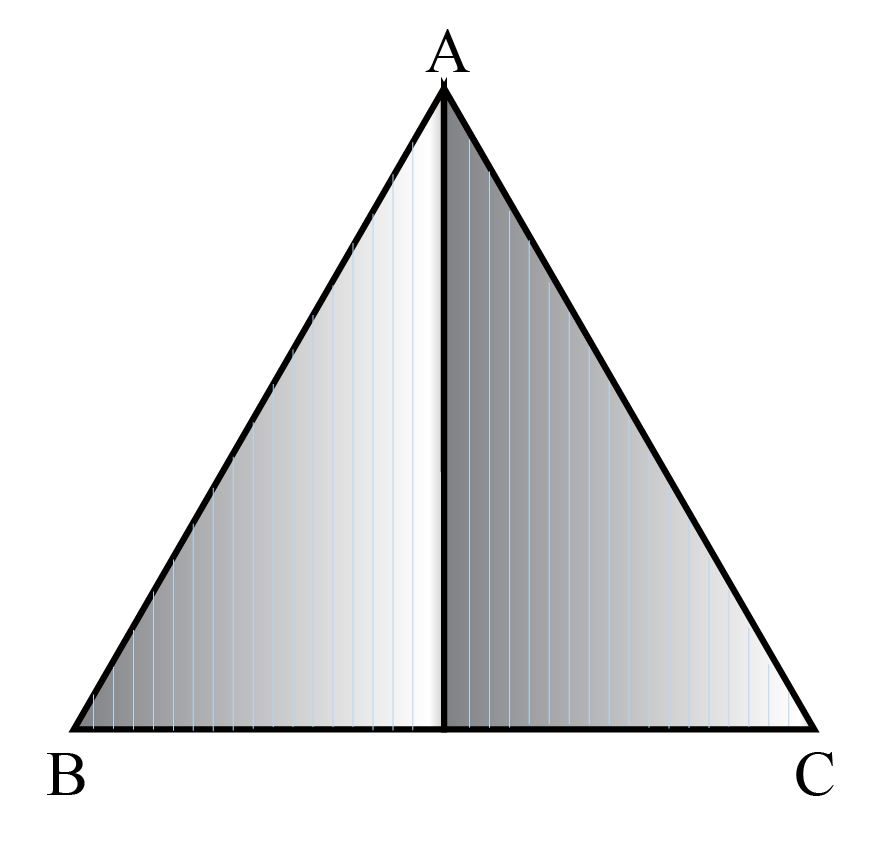
The name derives from the Greek iso (same) and skelos (leg). Next we construct a line perpendicular to the angle bisector and through point J. In an isosceles right triangle, the equal sides make the right angle. An isosceles triangle therefore has both two equal sides and two equal angles. Using the point tool we constructed point J that lies on the angle bisector. Lastly we can construct an isosceles triangle using rays. We can observe that if we move point F the triangle remains an isosceles triangle. Note, in an equilateral triangle, all three interior angles are identical to one another, and all three side lengths are equal to one another. An equilateral triangle is a special case of isosceles triangles. It follows that the two angles opposite to the two equal sides are equal in measure. An obtuse isosceles triangle is an isosceles triangle with a vertex angle greater than 90. Therefore triangle DFF' is an isosceles triangle. An isosceles triangle is one having two of its sides equal in length. An isosceles triangle is a triangle with two sides of equal length (and two angles of equal measure). Also we can see from the distance tool that DF and DF' are equal. Using the angle measure tool we can see that the measures of and are equal. Using the segment tool we construct DF FF' and F'D. Then we will reflect point F over segment DE to form F'. Construct segment DE and point F not on DE. We can also construct a isosceles triangle with a segment. We can move point C anywhere along the circle and the triangle is still an isosceles triangle. When we measure the angles measures and the side lengths of the triangle and see that the measures of and are equal and CA and AB are equal. Then using the segment tool we can construct segments AB, BC, CA to form triangle ABC. Then we also construct radius AC with C being a point anywhere on the circle.
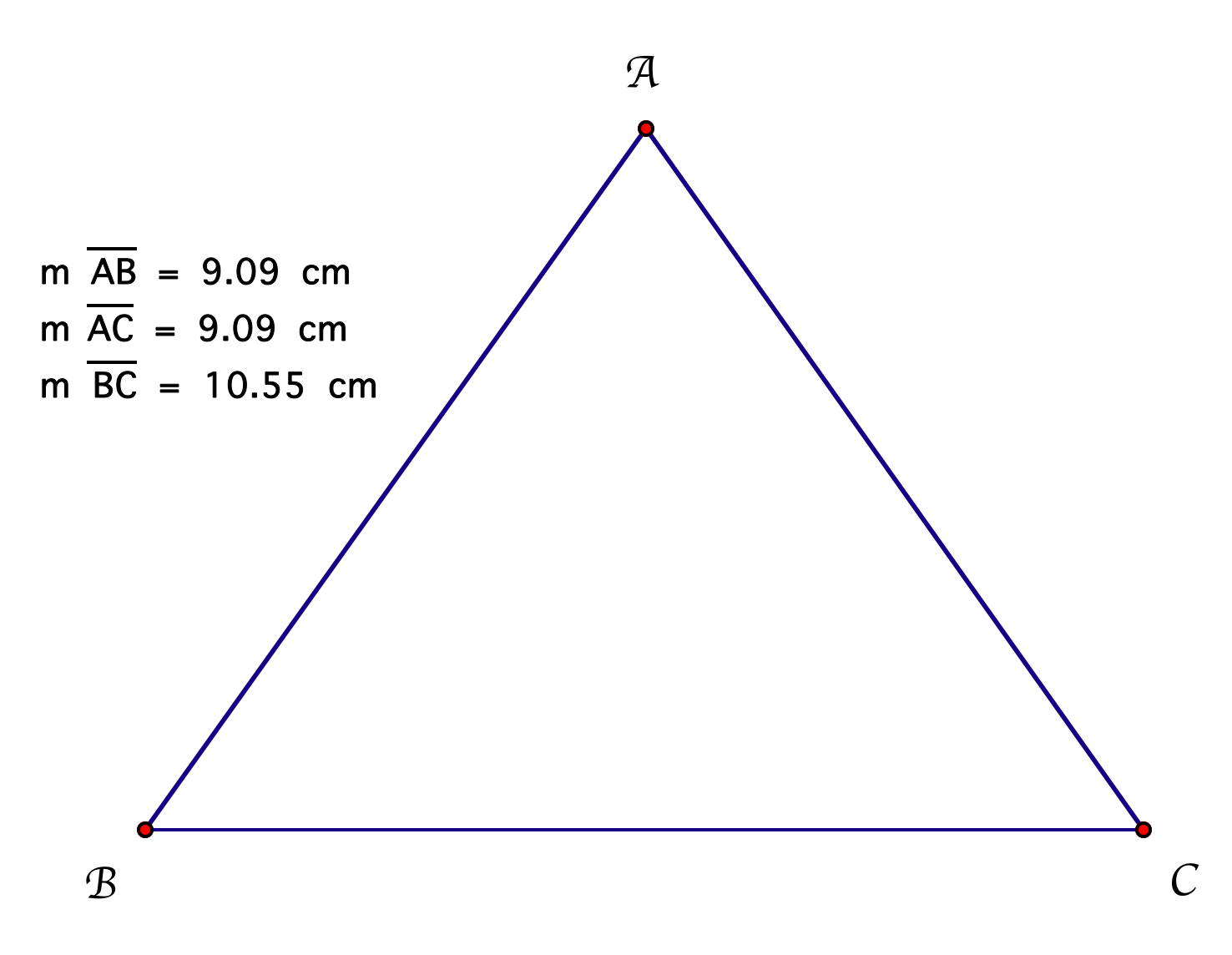
Then we construct the radius AB using the segment tool. Equilateral triangles have 3 equal sides and 3 equal angles of 60°. First we construct circle A using the circle tool. Notice that all equilateral triangles are isosceles. According to English language, the word isosceles means two sides. Definition: An isosceles triangle is defined as a triangle having two congruent sides or two sides that are the same length. An isosceles triangle is a triangle which has at least to sides equal to each other. For a triangle to be isosceles it has two sides of equal lengths and two angles of equal measure. A triangle that has two sides of equal length is called an isosceles triangle.


 0 kommentar(er)
0 kommentar(er)
